Error in Conway's "Regular Algebra and Finite Machines"
I was following “Proof Pearl: Regular Expression Equivalence and Relation Algebra” (Krauss & Nipkow, 2012) to implement a regular expression equivalence checker in OCaml to validate it as a project idea for my “Advanced Topics in Automata, Languages and Compilers” course.
Once the neat implementation was done, I wanted to test it, especially with pairs of regular expressions that aren’t trivially equivalent. I scoured the internet (mostly Stack Overflow) and the literature for such examples. Eventually I stumbled upon “Regular Algebra and Finite Machines” (Conway, 1971).
The error
Deep into the book, on page 121 it contains the following exercises:
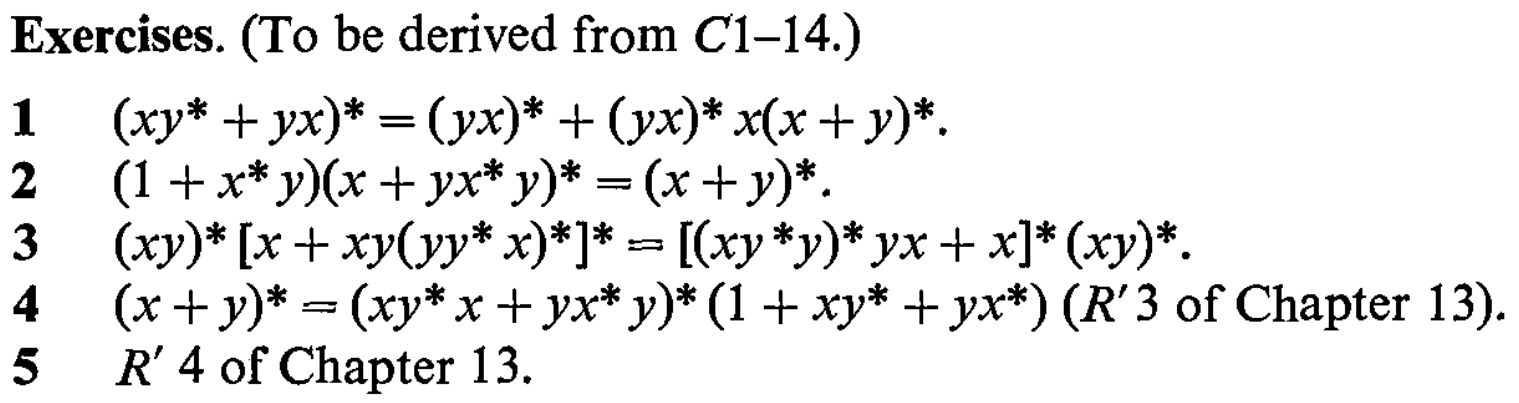
(Here \(+\) indicates the regex operator |, \(1\) is the empty string aka \(\varepsilon\) and \([]\) are just nested parenthesis for grouping, not a regex character class.)
Exercise 3 asks us to prove that (xy)*(x|xy(yy*x)*)* is equivalent to ((xy*y)*yx|x)*(xy)*. However, my checker didn’t agree and spat out the counterexample yx. Indeed, it’s not too hard to verify by hand that the first regex does not match yx while the second regex does. Hence, they aren’t equivalent!
The fix
The correct formulation of exercise 3 would be:
\[(\boldsymbol{yx})^*[x+xy(yy^*x)^*]^* = [(xy^*y)^*yx+x]^*(xy)^*.\]The difference compared to the book is shown in bold: beginning of the left-hand side should have yx instead of xy. My checker agrees that the two are now equivalent.
This is indirectly corroborated later in the book as well. Solutions to the exercises say:
A proof of 3 (not from C1-14) is implicit in later exercises.
And exercise 9 includes the fixed left-hand side regular expression.